Waiting Lines

What appears below is the first model in the book (from Chapter 2, Section 1). This model is very simple; much more elaborate models are possible. The goal here is just to give you a feel for how SimQuick works. Explanations of the details (including an introduction to simulation) can be found in the book.

Example: A bank

Consider the following process within a small bank: Customers enter the bank, get into a single line, are served by a teller, and finally leave the bank. Currently, this bank has one teller working from 9 a.m. to 11 a.m. Management is concerned that the wait in line seems to be too long. Therefore, they are considering two process improvement ideas: adding an additional teller during these hours or installing a new automated check-reading machine that can help the single teller serve customers more quickly.

What should management do?

To answer this question, management has collected and summarized some data:

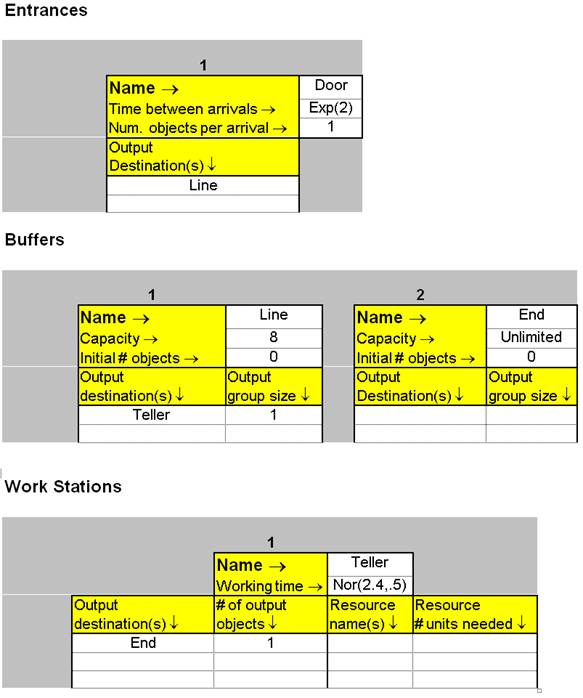
The amount of time between arrivals of customers can be approximated by an exponential distribution with a mean of 2 minutes. The line in this bank can only hold 8 people and if a person arrives when the line is full, he/she does not get in line. The service time by the teller can be approximated by a normal distribution with a mean of 2.4 minutes and a standard deviation of .5 minutes.

Building the model

Next we see how to build a SimQuick model for the current process with a single teller.

SimQuick provides five building blocks, called Elements, which can be combined in a huge number of ways. The elements are Entrances, Exits, Buffers, Workstations, and Decision Points.

The first step in using SimQuick is to draw a flow map of the real-world process using these building blocks. Here’s what the model looks like for the bank:

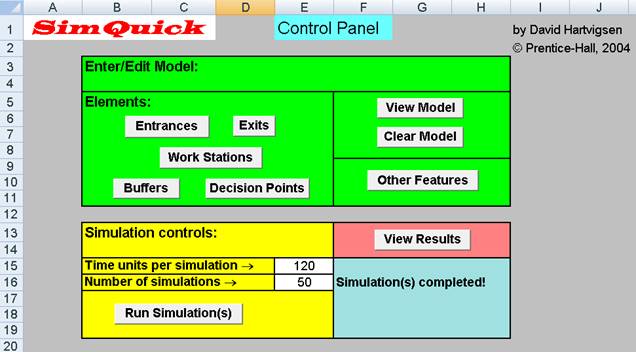
The next step is to input the model into SimQuick in Excel. You first open the Excel file SimQuick-v2.xls. What you see is the Control Panel, which is copied below. For each element in the model, you click on the element’s button on the Control Panel and fill in a table with the details about the element. You also fill in, on the Control Panel, how many simulations you want to do and how long each simulation should last. (In this example, we are doing 50 simulations, each for 120 time units, which corresponds to two hours.) The filled-in Control Panel and tables look like this:

Running and analyzing the model

You then click Run Simulations on the Control Panel. It takes SimQuick just a few seconds to simulate the 9AM to 11AM time period at the bank 50 times. Clicking on View Results brings up the table below. (Here we see only the results of the first five simulations.)

Simulation Results
Element	Element	Statistics	Overall	Simulation number(s)
types	names		means	1	2	3	4	5
Entrance(s)	Door	Objects entering process	53.88	58	56	55	57	48
		Objects unable to enter	6.70	7	3	6	18	0
		Service level	0.90	0.89	0.95	0.90	0.76	1.00
Work Station(s)	Teller	Final status	NA	Working	Working	Working	Working	Not Working
		Final inventory (int. buff.)	0.00	0	0	0	0	0
		Mean inventory (int. buff.)	0.00	0.00	0.00	0.00	0.00	0.00
		Mean cycle time (int. buff.)	0.00	0.00	0.00	0.00	0.00	0.00
		Work cycles started	48.43	51	49	49	50	48
		Fraction time working	0.96	0.98	1.00	0.97	0.97	0.96
		Fraction time blocked	0.00	0.00	0.00	0.00	0.00	0.00
Buffer(s)	Line	Objects leaving	48.43	51	49	49	50	48
		Final inventory	5.45	7	7	6	7	0
		Minimum inventory	0.00	0	0	0	0	0
		Maximum inventory	7.77	8	8	8	8	7
		Mean inventory	4.47	5.03	4.64	3.05	6.43	3.42
		Mean cycle time	11.04	11.83	11.36	7.46	15.43	8.54
	End	Objects leaving	0.00	0	0	0	0	0
		Final inventory	47.44	50	48	48	49	48
		Minimum inventory	0.00	0	0	0	0	0
		Maximum inventory	47.44	50	48	48	49	48
		Mean inventory	22.75	22.84	24.19	22.71	23.29	22.89
		Mean cycle time	Infinite	Infinite	Infinite	Infinite	Infinite	Infinite

From this table you can see two key performance measures: Our simulated customers were waiting in line for 11.04 minutes, on average (see the “Mean cycle time” row under “Buffer(s), Line”), and there were 4.47 customers in line, on average (see the “Mean inventory” row under “Buffer(s), Line”).

From here it’s easy to change the model for the case of two tellers and the case of a single teller who can work faster due to some automation. We can then see the effect of these changes on the waiting time and number of customers in line. This can help management decide what to do.

See the book for the details.